10.22.2023
0. Introduction
Linear Regression은 가장 심플한 모델들 중에 하나다.
이 모델을 학습하는데에는 2가지 방법이 있다.
1. A direct closed-from equation. 다이렉트하게 코스트 펑션을 최소화하는 파라미터를 계산.
2. Gradient Descent, which is an interative optimization. 모델 파라미터를 조금씩 변경하면서 코스트 펑션을 최소화하는 파라미터를 찾아내는 기법
1. Linear Regression
리니어 리그레션은 인풋 피쳐에 대한 가중치를 가진 총합과 바이어스 텀(Bias Term)이라는 상수값으로 예측을 만드는 모델
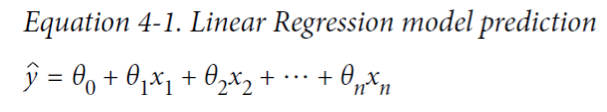

y=f(x)라는 함수가 있을 때, 우리가 아는 것은 x, y가 포함된 데이터셋이며, 목표는 f를 찾는 것이다.
노이즈와 널데이터 등을 이유로 완벽한 f를 찾는 것은 힘들다.
결국 세타라는 파라미터를 가진 h펑션(f와 가장 비슷한)을 찾는게 우리의 목표이다.
그러므로 결과값은 정답값이 아니고 예측값이기 때문에, 표기될 때는 y가 아닌 y^(y햇)으로 표기된다.
위의 식을 벡터식으로 바꿨을 때


벡터로 바꾼 이유는, 매트릭스같은 행렬로 입력해주면 더 효과적이기 때문.
1-1. 리니어 리그레션을 트레이닝 하는 방법
모델을 트레이닝한다는 의미는 트레이닝 데이터에 가장 fit되는 파라미터를 찾는 행위이다.
처음에는 첫 모델이 얼마나 데이터에 피팅되는지 보고(Root Mean Square Error, RMSE를 이용해서)
RMSE를 최소화하는 세타값을 찾는 것이 리니어 리그레션을 트레이닝 하는 방법이다.
RMSE값은 작을 수록 좋은데, 수식적으로는 미분해서 0이 되는 지점을 찾으면 된다.
현실적으로는 RMSE보다 MSE를 최소화하는게 더 쉬우며, 같은 결과값을 내기 때문에 MSE를 최소화한다.(똑같은 기울기 패턴을 가지기 때문)

그라운드 트루스(y(i))와 프리딕션값 (세타 * x(i))의 차이의 제곱을 다 더하고 m으로 나눈 중간값이 MSE이다.
1-2. Normal Equation
리니어 리그레션 모델을 학습시킬 수 있는 closed-form 방식. 코스트 펑션을 최소화하는 세타를 바로 찾을 수 있다.

노멀 이큐에이션으로 세타를 찾는 코드


찾은 세타를 이용해 프리딕션을 하는 코드

Normal Equation의 단점
노멀 이큐에이션은 기본적으로 XTX피쳐의 갯수가 두 개가 되면, 계산에 걸리는 시간이 5배-8배까지 올라감(O(n2.4) to O(n3).
SVD를 이용해도 O(n2)정도임.
물론 이 둘의 장점은 m, 데이터 포인터의 갯수에 대해서는 리니어하게 올라감(O(m)). 데이터 포인터 갯수의 증가는 괜찮은 편.
이 단점을 극복하기 위해 나온게 Gradient Descent
2. Gradient Descent (Interactive)
2-1. Gradient Descent 기본 설명
피쳐가 많을 때나 메모리에 트레이닝 인스턴스를 한 번에 다 올리기 어려울 때(Normal Equation이 불가능할 때) 사용.
대부분의 기계학습은 Normal Equation과 같이 direct하게 세타를 찾는 방법보단 그라디언트 디센트와 같이 interactive한 방식을 더 많이 사용.
그라디언트 디센트는 다양한 문제에 대해 최적의 솔루션을 찾는데 최적화된 알고리즘이다.
이 알고리즘은 에러 펑션에 대한 로컬 기울기를 측정하고, 내려가는 기울기 방향으로 내려간다.
그라디언트(기울기)가 0이 되면, 최소값에 도달했다고 볼 수 있다.
처음 초기값은 랜덤값이다.
코스트 펑션을 감소시키기 위해 작은 보폭의 스텝을 취한다. 알고리즘이 최소값에 닿을 때까지.

한 스텝의 사이즈는 Learning Rate이라고 부른다.
이 러닝레잇은 하이퍼 파라미터이며 상수값인데, 학습되면서 변화하는 variable이 아니라는 뜻이다. 유저가 설정하는 값.
이 러닝레잇이 너무 작으면 이터레이션이 많아서 오래걸린다. 최소값에 도달하는 것이 불가능하지는 않음.
다만 러닝레잇이 너무 크면 diverge, 발산할 수가 있다. 이 경우에는 최소값에 도달하는 것이 불가능.
가장 좋은건 이 중간의 어느 적절점이지만, 너무 큰 러닝레잇은 워스트케이스라고 할 수 있다.

최종적으로 코스트 펑션의 형태가 가장 중요하다. 그릇 모양처럼 convex한 형태가 가장 좋음.
만약 코스트 펑션이 holes(구멍), ridges(산등성), plateaus(고원, flat함을 의미)와 같은 지역이 있으면 미니멈에 도달하기가 쉽지 않음.
예시

랜덤 초기화를 진행하면 왼쪽의 경우(그래프에 굴곡이 있는 경우) local minimum에 빠질 위험이 있음.
오른쪽의 경우(그래프가 flat한 경우) 시간이 너무 오래 걸릴 수 있음.
다행히도, 리니어 리그래션 모델들에서의 MSE cost function은 convex function이다. 로컬 미니멈은 없고 글로벌 미니멈만 존재.
MSE cost function이 찌그러진 그릇 모양일 수도 있음. 이럴 경우를 대비해 GD를 이용할 때는 피쳐 스케일을 해줘야 함
결론적으로 Learning Rate을 적절히 잡는 것과 글로벌 미니멈을 찾을 때까지 충분히 기다리는 것이 Linear Regressionp에서의 키이다.
2-2. Batch Gradient Descent
배치 그라디언트 디센트는 데이터를 한 번에 메모리에 올리는 방식이다.
이 경우, 한 스텝에 전체 트레이닝 셋이 다시 계산됨.
피쳐의 갯수가 많은 데이터 셋의 경우, 스케일 성능이 매우 뛰어남(Normal Equation/SVD 단점 보완)
그러나 데이터가 크면 엄청엄청 오래 걸리고, 메모리도 데이터보다 커야함.

좋은 러닝 레이트를 찾기 위해서, 그리드 서치를 사용할 수 있다. 다른 하이퍼파라미터를 찾을 때도 사용 가능
이터레이션의 횟수를 정할 때는 엄청 큰 숫자를 이터레이션 넘버로 잡고, 그라디언트가 0에 가까워졌을 때 알고리즘을 멈추는 방법이 가장 단순한 솔루션이다.
2-3. Stochastic Gradient Descent
배치 그라디언트 디센트의 경우, 너무 느린게 단점임. 그래서 스토캐스틱이 나옴.
스토캐스틱 그라디언트 디센트는 매 스텝마다 랜덤 인스턴스를 고르는 기법이다.
학습시간이 훨씬 짧아지고, 메모리에 모든 데이터셋을 한 번에 올리지 않아도 된다는 장점이 있다.
다만 랜덤하게 데이터를 뽑기 때문에 그래프가 훅 내려가거나 훅 올라가는 가파른 느낌이 될 수 있다. (전체적으로는 내려가긴 함)
알고리즘이 멈췄을때 최종 파라미터 값이 좋을 수는 있지만, 최적의 값은 아닐 수 있다. (왔다갔다 하면서 글로벌 미니멈에 도달하기 때문)
그렇지만 만약 코스트 펑션이 irregular 한 경우(convex하지 않은 경우) 오히려 로컬 미니멈을 벗어날 수 있는 가능성이 있음.
이 경우의 해결책은 러닝 레잇을 점차적으로 reduce하는 것이다.
너무 빠르게 줄이면 로컬 미니멈에 갇히거나 플랫한 부분에 프로즌 될 수 있고, 너무 느리게 줄이면 발산되거나 글로벌 미니멈 근처에서 점핑하며 맴돌 수도 있다.
각 이터레이션에서의 러닝레잇을 결정하는 함수를 learning schedule이라고 한다.
그래서 m 번의 tieration을 한다고 칠때, 한 번의 이터레이션을 epch, 에포크라고 한다.
배치 그라디언트의 경우 1천번정도가 필요하지만, learning schedule과 epoch를 이용하면 50번만 해도 좋은 결과를 얻을 수 있다.

스토캐스틱 그라디언트 디센트를 쓸 때는, 트레이닝 인스턴스들은 independent(독립적)하고 Identically distributed(동일하게 분산)되어야 한다. => IID

2-3. Mini-batch Gradient Descent
미니배치 그라디언트 디센트는 mini-batch라고 불리는 작은 랜덤 인스턴스 셋에 대해 그라디언트를 계산하는 방식이다.
배치와 스토캐스틱의 중간쯤 되는 방법.
둘다 글로벌 미니멈 주변에서 맴돌기는 하지만 하드웨어 부분에서 스토캐스틱보다 장점이 있음.
2-4. Gradient Descent 총정리

3. Phlynomial Regression
Non-linear 데이터에도(차원이 높음 등) 리니어 모델을 사용할 수 있다.
폴리노미얼 리그레션은 이럴때 사용하는 가장 단순한 방법이다.
인풋 피쳐들에 높은 차원의 피쳐를 새로운 인풋 피쳐로 추가하여 리니어처럼 웨이트를 학습시키는 방식이다.
만약 피쳐가 여러개가 있다면, 폴리노미얼 리그레션은 피쳐 사이의 관계를 찾는 것도 가능하다.(주어진 차원에 대해 모든 콤비네이션을 만들기 때문에)(a,b 가 있을 때 a, a2, b, b2 뿐만 아니라 ab, a2b, ab2도 추가함)
최종적으로 피쳐의 갯수는 (n+d)!/d!n!이 됨 (d: degree, n: features)
피쳐의 갯수가 늘어나면 익스플로젼(폭발)이 발생할 가능성도 염두에 두어야함
4. Learning Curves (러닝커브를 알아야 언제가 최적의 타이밍인지 알수 있음)
모델이 얼마나 복잡해야 하는지 어떻게 결정할 수 있을까?
High-degree Polynomial Regression은 plan Linear Regression보다 트레이닝 데이터에 피팅이 더 잘 될거임(더 복잡하기 때문)
그치만 모델이 너무 복잡하면 오버피팅이 일어나게 되고, 너무 단순하면 언더피팅이 일어나게 됨.
결과적으로 우리는 차원(디그리), 즉 가설의 형태를 미리 결정해야하는데 이것이 굉장히 어려움. 그럼에도 두 가지 방법이 있다면
- 크로스 벨리데이션을 사용해서 퍼포먼스를 확인한다.
- 러닝커브를 확인한다.
예시: plain Linear Regression model

그래프의 가장 앞부분에서는 모델이 퍼펙트핏이기 때문에 0에서 시작하며, 데이터가 추가될수록 단순한 모델로는 완벽하게 피팅하는게 불가함. 일정 시점이 지나면 플랫하게 되어 좋아지거나 나빠지지 않음.
이 그래프에서 벨리데이션과 트레이닝 사이의 커브가 굉장히 가깝고 플랫한 구간이 긴 것을 확인할 수 있는데, 이것은 언더피팅의 특징임.
결론적으로 언더피팅되어있는 것을 확인할 수 있고, 모델의 복잡도를 올려야 함.
예시: 10th degree polynomial model

이전 그래프와의 차이점
- 트레이닝 데이터셋에 대한 에러가 전 모델보다 훨씬 낮음
- 벨리데이션/트레이닝 커브의 갭이 큼
2번의 경우 발리데이션보다 트레이닝 데이터셋에 더 잘 반응한다는 근거가 되므로, 오퍼피팅임을 알아낼 수 있다.
5. Regularized Linear Models
정규화(Regularization)
모델이 트레이닝 데이터셋에 오버피팅되는것을 막기 위한 과정이라고 할 수 있음.
정규화에서는 상반되는, tradeoff관계인 두 가지 goal이 있다.
- 프리딕션 에러를 줄이는 것 (이 경우 complexity가 높아져야 함)
- 최대한 심플한 모델을 만드는 것 (이 경우 complexity가 낮아져야 함)
이 두 가지 목표를 달성하려면 cost function을 잘 짜야함.
폴리노미얼 모델을 정규화하는 가장 단순한 방법은 디그리 수를 줄여 복잡도를 낮추면서 오버피팅을 예방하는 것이다. 하이디그리에 해당하는 데이터를 0으로 처리한다.
리니어 모델을 정규화하는 방법은 모델의 가중치에 제약을 거는 방식이다.
5-1. Ridge Regression
릿지 리그레션이란 Regularization term(세타)을 코스트 펑션에 더한 것이다.


정규화의 목적은 코스트 펑션을 줄이는 게 목적이다. 결론적으로 세타i를 줄이는게 릿지 리그레션에서의 정규화의 목적이다.
하이퍼파라미터 알파는 얼마나 모델을 정규화 할 것인가를 나타낸다. 적절한 수준에서 컨트롤되어야 함.
알파가 너무 크면 거의 flat한 모델이 되고, 알파가 0이면 릿지 리그레션이 그냥 리니어 리그레션이랑 똑같게 됨.

리니어 리그레션은 인풋 피쳐의 스케일에 민감해서, 사용하기 전에는 데이터를 스케일링 하는 것이 중요하다.
사실 정규화를 진행하는 모든 모델은 인풋 피쳐 스케일이 필요하며, 리그레션의 경우에는 더더욱 중요하다.
5-2. Lasso Regression
라쏘 리그레션은 코스트 펑션에 세타의 절대값을 더한 리그레션이다.
릿지 리그레션은 L2, 라쏘 리그레션은 L2 norm을 쓴다.

위에 릿지 리그레션에서도 보았듯이, i가 1부터 시작하는 이유는 바이어스 텀은 정규화를 하지 않기 때문임.
릿지와 비교해서 가장 중요한 차이점은, 라쏘 리그레션은 중요하지 않은 피쳐의 세타값을 0으로 세팅할 수 있다는 것이다.(웨이트를 0으로 줌)
라쏘 리그레션을 이용하면 피쳐를 자동으로 선택할 수 있는 모델이 생성된다.

여기서 컨투어는 cost function 값이다.
라쏘에서는 특정 세타들이 0으로 수렴하는 방향성을 보이고, 무의미한 세타들은 탈락하는 반면
릿지에서는 세타들이 작아지기는 하지만 0으로 가지는 않고 같은 방향으로 작아진다.
5-3. Elastic Net
엘라스틱 네트는 릿지 리그레션과 라쏘 리그레션의 중간에 있다.
엘라스틱 네트의 regularization term은 단순히 릿지와 라쏘를 합쳐놓은 모양이 된다.
이때 믹스 레이시오 r을 이용해서 어느쪽을 더 믹스할지 컨트롤 할 수 있는데, r=0이면 릿지가 되고, r=1이면 라쏘가 된다.

바이어스는 역시 정규화가 진행되지 않으며, 알파의 의미 역시 같다(얼마나 정규화를 진행할지)

5-3. Early Stopping
GD와 같은 인터랙티브한 학습 알고리즘을 정규화하는 또 다른 방법은 발리데이션 에러가 최소값일 때 학습을 멈추는 것이다.
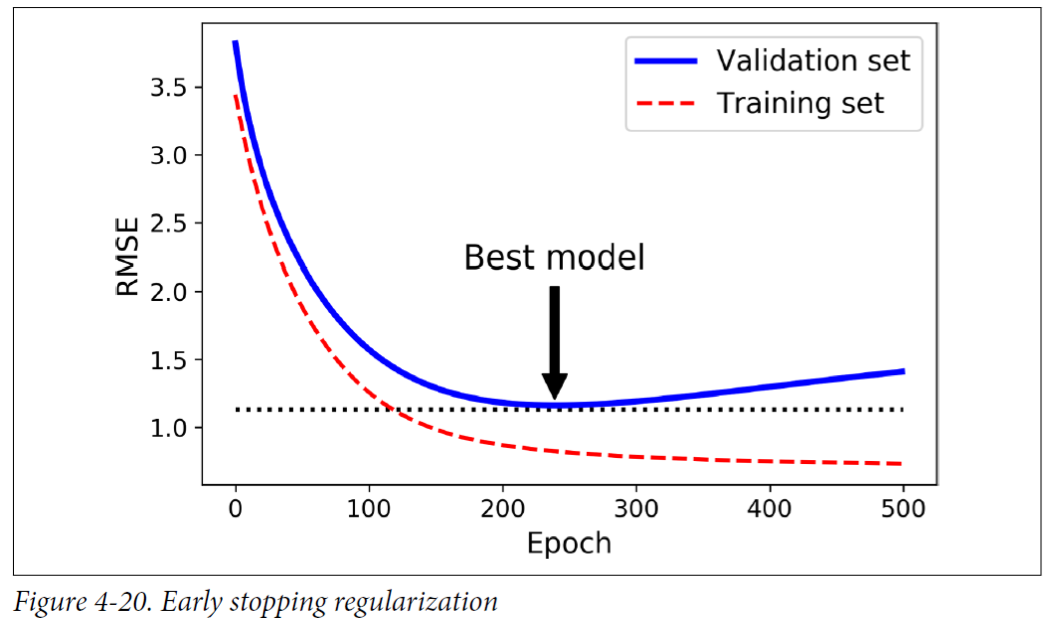
RMSE를 최대한 줄이는 방향으로 학습한다. 만약 RMSE가 줄어들지 않는다면 코드에 문제가 있는 것.
미니배치나 스토캐스틱의 경우는 다를 수 있지만, 데이터가 한 번씩 발리데이션이 된다는 가정 하에, MSE는 무조건 떨어져야 한다.
그렇다고 무조건 많이 학습하는 것이 좋은 것은 아니다.
한 에포크가 끝날 때마다 발리데이션 에러 결과를 보고, 발리데이션은 작아지다가 다시 상승하는 지점이 생기는데 그 지점이 발리데이션 에러의 최소값을 의미하지는 않는다.
결론적으로, 각 모델 트레이닝이 끝났을 때 모델을 중간 중간 세이브해줘야 함.
6. Logistic Regression(확장하면서 리그래션에서 클래시피케이션으로 바꿀 수 있음)
로지스틱 리그레션은 이름만 리그레션이고 사실 바이너리 클래시피케이션 문제를 위한 알고리즘이다.
리그레션이라는 이름이 붙은 이유는 앞에서 우리가 본 리그레션과 똑같은 모델을 사용해서 클래시피케이션을 할 수 있기 때문이다.
6-1. Estimating Probabilities
바이너리 클래시피케이션에서, 0일 확률과 1일 확률을 계산해서 더 높은 스코어를 피팅하는 것이 컨셉이다.
다른 리니어 리그레션 모델처럼, 로지스틱 리그레션 모델은 인풋피쳐의 가중치합을 계산하지만, 리니어 리그레션 모델처럼 결과값을 바로 내보내는게 아니라, '로지스틱'을 한 번 거친 후 아웃풋을 낸다.

이 함수는 0과 1사이로 바운딩된다.
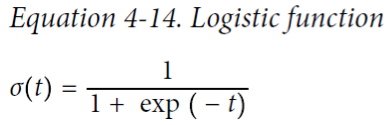
로지스틱 리그레션은 시그모이드 함수이다.

이 시그모이드 함수가 0.5보다 크면 1이고, 작으면 0이 된다.
6-2. Training and Cost Function
학습의 목표는 네거티브 인스턴스에 대해서 최대한 작은 프라바빌리티를 출력시키고, 파지티브 인스턴스를 위해서는 최대한 큰 프라바빌리티을 예측하도록 파라미터 벡터인 세타를 학습시키는 것이다.
코스트 펑션을 모든 트레이닝 셋에 대해 평균화해야 그레디언트 디센트같은 방식으로 작아지게 할 수 있음.
안타깝게도 코스트 펑션을 최소화시킨느 세타의 값을 찾는 closed-form equation은 알려지지 않았다.
다행히도 코스트 펑션은 convex하기 때문에 GD를 쓸 수 있고, 글로벌 미니멈을 찾을 수 있음이 보장되어 있다.
6-3. Decision Boundaries
디시전 바운더리를 찾는다는 것은 프라바빌리티가 0.5인 바운더리를 찾는다는 것을 의미한다.

아이리스 데이터를 이용해 로지스틱 리그레션을 적용해 본 결과이다.
페탈 랭스가 2센치보다 높으면 확실히 아이리스가 맞고, 1센치보다 작으면 아닌데, 가운데는 불확실함.
1.6 정도에 디시전 바운더리가 생기는 것을 볼 수 있음
6-4. Softmax Regression
로지스틱 리그레션 모델은 멀티플 클래스에 대해 클래시파이 할 수 있도록 일반화시킬 수 있는데, 이것을 소프트맥스 리그레션이라 한다.
주어진 인스턴스가 있을 때, 각 클래스에 대해 스코어를 계산하고, 그 스코어를 기반으로 펑션에 넣어 각 클래스의 확률을 계산한다.
스코어 일반화라고 보면 됨.

스코어를 모두 구했을 때는 소프트맥스 함수를 통해 프라바빌리티를 결정한다.

k: 클래스의 갯수
s(x): 인스턴스 x에 대한 각각의 클래스의 스코어를 가지고 있는 벡터
𝞼(s(x))k: 계산된 확률

스코어를 계산하는 부분에서의 k와 소프트 맥스 함수를 통과한 다음의 k는 똑같음(클래스의 갯수는 변하지 않음)
소프트맥스 리그레션의 목표는 타겟 클래스에 대해 높은 확률을 계산하는 모델을 만드는 것(다른 클래스들에게는 낮은 확률)
예시: 아이리스 데이터 / 세개의 클래스 모두 적용

multi_class="multinomial": 소프트맥스 리그레션으로 스위치
C=10: 얼마나 정규화를 진행할 것인지에 대한 하이퍼 파라미터

결과값

94.2퍼센트의 확률을 갖는 것을 볼 수 있다.
'CS > ML' 카테고리의 다른 글
| [ML] 요점정리 (1) | 2023.10.25 |
|---|---|
| [ML] 5주차 - SVM (1) | 2023.10.23 |
| [ML] 머신러닝 3주차 - Classification (2) | 2023.10.08 |
| [ML] 머신러닝 2주차 복습 정리 (1) | 2023.10.01 |
| [ML] 머신러닝 1주차 복습정리 (0) | 2023.09.17 |


